「题解 P6830」IOI2020 连接擎天树

November 25, 2020

2020   ·   OI   Chinese     ·   pre-university  

这题主要的难点是交互题的形式……调试了快一年

首先我们注意到一个奇怪的数据限制: $p[i][j]\in [0,3]$, 这样的话, 我们可以证明: 对于两个有路径的节点, 他们一定位于一棵树或一棵基环树上

一个联通的无向图可以看作在一棵树的基础上加 $k$ 条边

当 $k=1$ 时, 是一棵基环树

此时, 我们可以发现, 环上各点相互之间都有 $2$ 条互通路径, 而环上连接的树内两两只有 $1$ 条路径

如果我们再加入另一条边 $4-7$: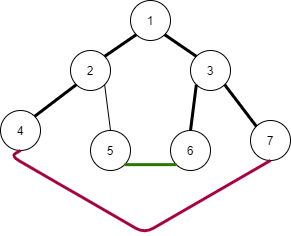

则一定会形成两个新的环($1-2-3-7-3$ 与 $2-4-7-3-6-5$)

此时, 除了对于原环上的一点 (除了 $2,3$ 两个和 $4,7$ 原来有且只有一条路径的) , 我们能找到至少 $4$ 条到 $4$ 或 $7$ 的路径 (即: 原先通往 $2$ 与 $3$ 的四条路径, 再在 $2$ $3$ 的子树上走到对应的另一棵子树上的 $7$ $4$)

所以可以保证每一个连通块都是树或基环树, 且最大的路径树应为 $2$, 所以出现 $3$ 的情况可以直接排除

对于一个最大路径数为 $1$ 的连通块, 直接建树即可

对于一个最大路径数为 $2$ 的连通块, 根据上面对于基环树的分析, 我们对每个以环上一点为根的子树 ($2-4$ 与 $3-7$) 单独建树, 再在每棵树上各取一点连成环即可

顺便贴一下测试数据与 $check$ 程序领取地址

代码:

#include <iostream>
#include <cstdio>
#include <vector>

using namespace std;

const int MAXN = 1005;

void build(vector<vector<int> > b);

int n, cnt;
int fa[MAXN], belong[MAXN], vis[MAXN];
vector<int> cir, edg;
vector<vector<int> > gr, tr, ans;

int find(int x) { return fa[x] == x ? fa[x] : fa[x] = find(fa[x]); }

void dfs(int u)
{
    vis[u] = 1;
    edg.push_back(u);
    for (int v = 0; v < n; v++)
        if (!vis[v] && gr[u][v] == 1)
            dfs(v);
}

int construct(vector<vector<int> > p)
{
    gr = p;
    n = p[0].size();
    tr.clear();
    ans.clear();
    tr.resize(n + 1);
    ans.resize(n);
    for (int i = 0; i < n; i++)
    {
        fa[i] = i;
        ans[i].resize(n);
    }
    for (int i = 0; i < n; i++)
        for (int j = i + 1; j < n; j++)
            if (p[i][j] != 0)
            {
                int fx = find(i), fy = find(j);
                if (fx != fy)
                    fa[fx] = fy;
            }
    for (int i = 0; i < n; i++)
    {
        find(i);
        if (belong[fa[i]])
            belong[i] = belong[fa[i]];
        else {
            belong[i] = ++cnt;
            tr[belong[i]].clear();
            belong[fa[i]] = cnt;
        }
        tr[belong[i]].push_back(i);
    }
    for (int i = 1; i <= cnt; i++)
    {
        int siz = tr[i].size();
        bool flag = 0;
        for (int j = 0; j < siz - 1; j++)
            for (int k = j + 1; k < siz; k++)
            {
                int u = tr[i][j], v = tr[i][k];
                if (p[u][v] == 3 || p[u][v] == 0)
                    return 0;
                if (p[u][v] == 2)
                    flag = 1;
            }
        if (!flag)
        {
            for (int j = 0; j < siz - 1; j++)
                ans[tr[i][j]][tr[i][j + 1]] = ans[tr[i][j + 1]][tr[i][j]] = 1;
        }
        else {
            cir.clear();
            for (int j = 0; j < siz; j++)
            {
                int u = tr[i][j];
                if (vis[u])
                    continue;
                edg.clear();
                dfs(u);
                int esiz = edg.size();
                for (int k = 1; k < esiz; k++)
                {
                    for (int l = 0; l < k; l++)
                        if (p[edg[k]][edg[l]] != 1)
                            return 0;
                    ans[edg[0]][edg[k]] = ans[edg[k]][edg[0]] = 1;
                    // printf("%d %d\n", edg[0], edg[k]);
                }
                // printf("%d\n", edg[0]);
                cir.push_back(edg[0]);
            }
            if (cir.size() <= 2)
                return 0;
            int csiz = cir.size();
            for (int j = 0; j < csiz - 1; j++)
                ans[cir[j]][cir[j + 1]] = ans[cir[j + 1]][cir[j]] = 1;
            ans[cir[0]][cir[csiz - 1]] = ans[cir[csiz - 1]][cir[0]] = 1;
        }
    }
    build(ans);
    return 1;
}